How To Find Instantaneous Rate Of Change From A Graph

The average charge per unit of modify represents the full change in one variable in relation to the full change of another variable. Instantaneous charge per unit of change, or derivative, measures the specific rate of change of one variable in relation to a specific, infinitesimally minor change in the other variable. The average rate of change of a office tin be determined with secant lines and the instantaneous rate of alter can be determined with tangent lines. As yous will learn, these rates tin can too exist determined using a special type of math called calculus.

What is the rate of alter?

Rate of alter is the change in one variable in relation to the modify in another variable. A common rate of change is speed, which measures the change in distance travelled in relation to the time elapsed. Olympic Gold Medalist, Usain Bolt, became the earth'southward fastest man running at a top speed of 44.72 km/60 minutes during the 100-meter dash. On average, his speed was a bit slower (all the same, very impressive) at 37.58 km/hour. Bolt's summit speed is an example of an instantaneous rate of modify, and his average speed is an boilerplate rate of change.

Average Rate of Change

Secant lines are found by connecting ii points on a bend. The slope of the secant line between 2 points represents the average rate of change in that interval.

Formula:

Average Rate of Change = Slope(m) = △y/△x = $\frac{y_{2} - y_{1}}{x_{2} - x_{1}}$ = $\frac{f(x_{1}) - f(x_{0})}{x_{1} - x_{0}}$

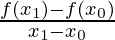
How to detect the average rate of alter between ii points using a secant line:

Step 1: Describe a secant line connecting the two points.

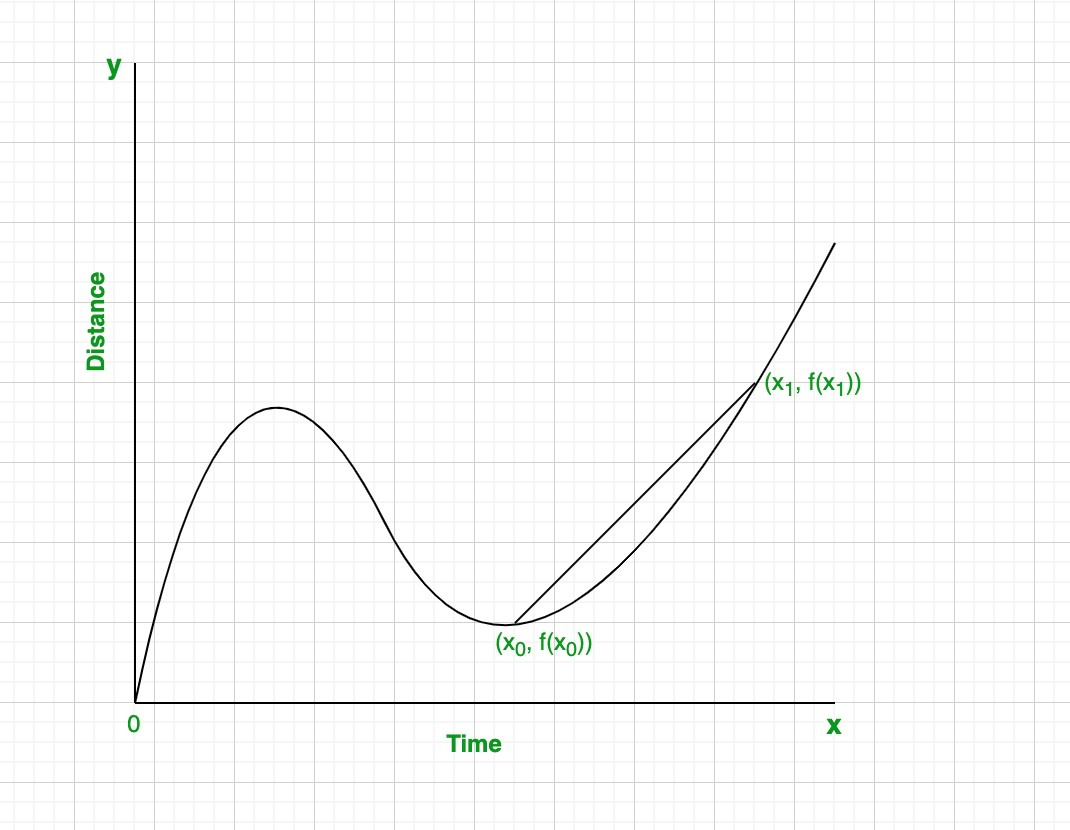
Step 2: Utilise the coordinates of the two points to calculate the slope.

Equation of gradient:
Slope =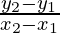 $\frac{y_{2} - y_{1}}{x_{2} - x_{1}}$

The average change of the office over the given time interval[10₀, x_one]
Slope =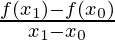 $\frac{f(x_{1}) - f(x_{0})}{x_{1} - x_{0}}$

The slope of the secant line represents the average
rate of modify of the graph in that interval.

Once you've calculated the slope of the secant line, you use the slope can write an equation to represent information technology.

For Instance:
Equation of gradient:
y – y₀ = g(ten – x₀)

m = slope of secant line = 4/7
10₀ = ii
y₀ = nine
$y - 9 = \frac{4}{7}(x -2)$

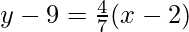
Hence, the equation of the secant line between x = ii and x = nine is
y – 9 =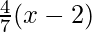 $\frac{4}{7}(x -2)$

Derivatives (Instantaneous Rate of Change)

The tangent line at a betoken is found by drawing a straight line that touches a curve at that point without crossing over the curve. In other words, the line should locally touch only one point. The gradient of the tangent line at a point represents the instantaneous charge per unit of alter, or derivative, at that point.

Formula:

Instantaneous Charge per unit of Alter = $f'(x_0) = \lim_{(x_0 \to x_1)} \frac{f(x_{1}) - f(x_{0})}{x_{1} - x_{0}}=\lim_{\triangle x \to 0} \frac{f(x_{0}-\triangle x) - f(x_{0})}{\triangle x}$

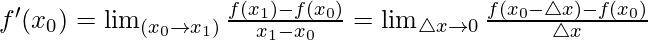
How to find the derivative at a point using a tangent line:

Step i: Draw a tangent line at the point.

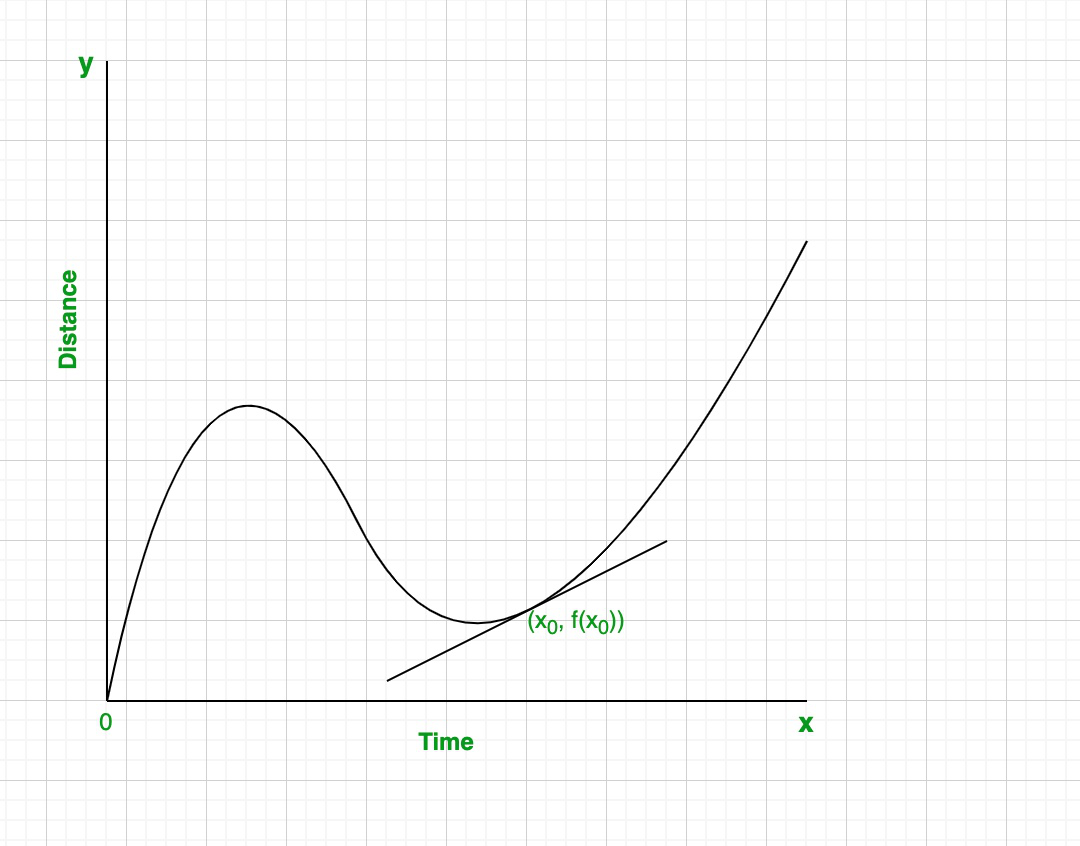
Step 2: Use the coordinates of whatever two points on that line to calculate the gradient.

Equation of gradient:
Gradient =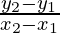 $\frac{y_{2} - y_{1}}{x_{2} - x_{1}}$

The average modify of the function over the given time interval ten₀
Slope =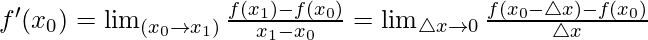 $f'(x_0) = \lim_{(x_0 \to x_1)} \frac{f(x_{1}) - f(x_{0})}{x_{1} - x_{0}}=\lim_{\triangle x \to 0} \frac{f(x_{0}-\triangle x) - f(x_{0})}{\triangle x}$

The slope of the tangent line at a betoken represents
the instantaneous rate of change, or derivative, at that indicate.

Once you've calculated the slope of the tangent line, y'all can write an equation to represent it.

For Example: Equation of slope:
y – y₀ = m(x – x₀)

m = gradient of tangent line = $\frac{5}{6}$
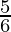
x₀ = sixteen
y₀ = half-dozen
$y - 16 = \frac{5}{6}(x - 6)$

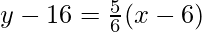
Hence, the equation of the tangent line at ten = 16 is
y – sixteen = \frac{v}{6}(x – 6)

Derivative Notation

In the early on 18th century, there was controversy betwixt the keen mathematicians Isaac Newton and Gottfried Wilhelm Leibniz over who the first invent calculus. This statement became known equally Prioritätsstreit, or "priority dispute" in High german. The disagreement has had lasting affect on the mathematical world, leaving us with two standard derivative notations. Lagrange notation is another common derivative note, established by French mathematician and philosopher, Joseph-Louis Lagrange.

If nosotros take the function y = f(x), So

1. Leibniz annotation:

"First derivative of y with respect to x"
⇒ $\frac{dy}{dx}$

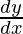
"2nd derivative of y with respect to ten"
⇒ $\frac{dy^2}{d^2x}$

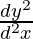
"First derivative of y with respect to x
at x = ii″
⇒ $\frac{dy}{dx}|_{x=2}$

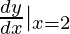
2. Newton notation:

The number of dots in a higher place the function
variable represents how many times the
function has been differentiated.
"Get-go derivative of y"
⇒ $\dot y$
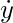
"Second derivative of y"
⇒ $\ddot y$
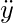
"Showtime derivative of y at ten = 2"
⇒ $\dot y (2)$

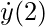
3. Lagrange notation:

The number of apostrophes after the office
variable represents how many times the
part has been differentiated.
"First derivative of y"
⇒y'
"First derivative of y at x = two"
⇒y'(2)
"Second derivative of y"
⇒y"

iv. Euler'due south notation

"Get-go derivative"
⇒ D₁₀f
"Second derivative"
⇒ D₁₀ ²f
Here, D represents the differential operator

Sample Issues

Question ane. Find the boilerplate rate of modify over the interval x = four, x = 6.

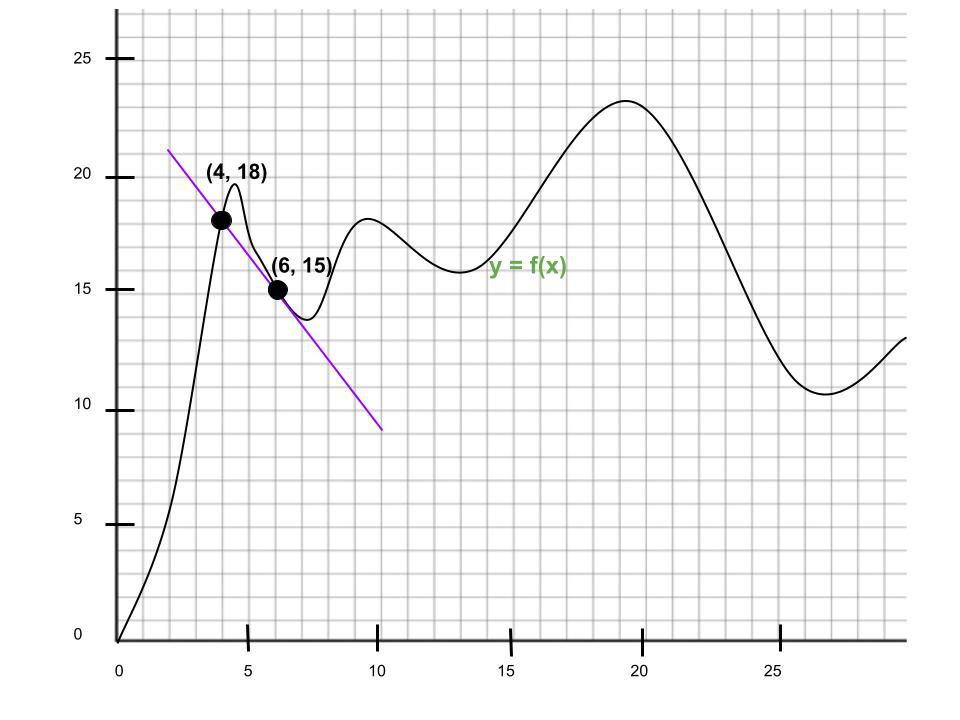
Solution:

Point ane: (4, 18)

Point 2: (6, 15)

Gradient = $\frac{y_{2} - y_{1}}{x_{2} - x_{1}}$

= $\frac{15 - 18}{6-4}$

= $-\frac{3}{2}$

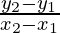
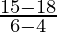
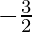
Hence, the average charge per unit of change = $- \frac{3}{2}$

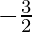
Question 2. Write the equation of the tangent line at 10 = 16.

Solution:

Betoken of intersection: (16, 18)

Gradient = $\frac{23 - 18}{18 - 16}$

= $\frac{5}{2}$

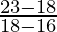
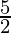
Equation of tangent line:

$y - 18 = \frac {5}{2}(x - 16)$

Question three. What is the derivative of the graph at x = xx? Express your answer in Leibniz notation.

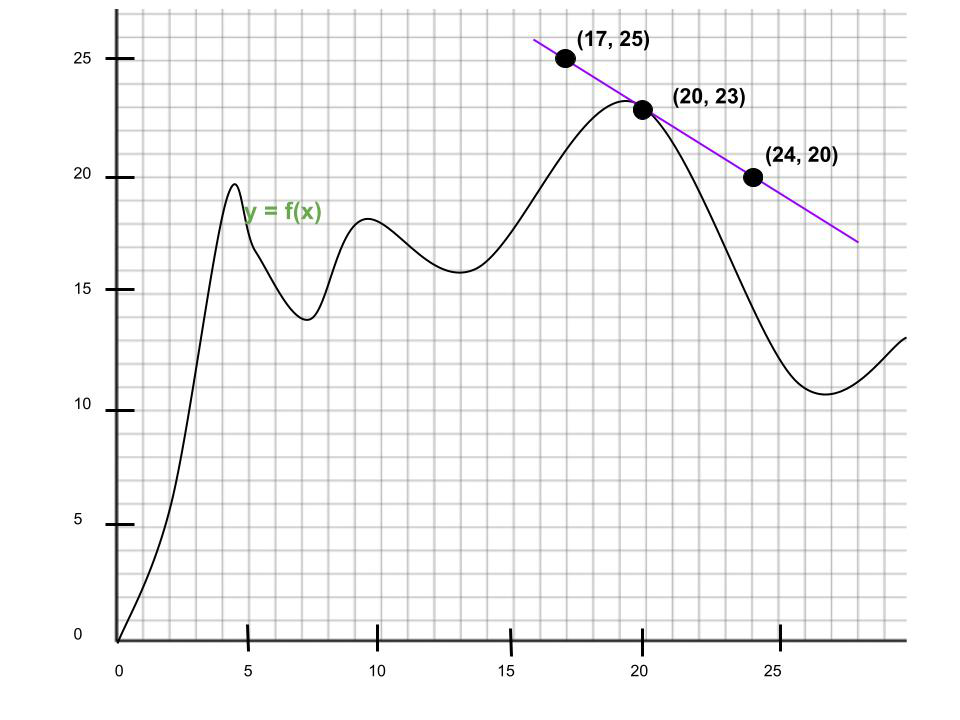
Solution:

Given point of intersection: (20, 23)

Gradient of tangent line = $\frac{20-25}{20-17}$

= $-\frac{5}{3}$

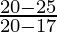
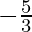
So, the Leibniz notation: $\frac {dy}{dx} | _{x=20} = -\frac{5}{3}$

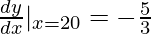
Question 4. Find the derivative of the graph at x = 4. Limited your answer in Newton'due south notation.

Solution:

Given indicate of intersection: (4, eighteen)

Slope of tangent line = $\frac{25 - 18}{7-4}$ = $\frac{7}{3}$

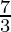
Then, the Newton'southward notation $\dot y(4) = \frac{7}{3}$

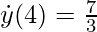
Question five. Find the boilerplate rate of alter over the interval x = 4, x = 25. How does this compare to the derivative at x = iv?

Solution:

Slope of secant line = $\frac {12 - 18}{25-4}$

= $- \frac{6}{21}$

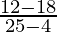
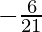
The average rate of change over x = iv, x = 25 is -6/21,

which is less than the derivative of y at x = 4, which we found to

be 7/three.

Question 6. Observe the instantaneous rate of modify of the given function f(x) = 2x² + 18 at x = nine ?

Solution:

Given: f(x) = 2x^two + eighteen

f'(x) = 4x + 0

f'(x) = 4x

Now we take to find the instantaneous rate of modify at x = 9

f(9) = 4x

f(9) = 4(ix)

f(ix) = 36

Question 7. Find the instantaneous rate of change of the given office f(x) = 4x² + 12x + viii at x = four ?

Solution:

Given: f(x) = 4x^two + 12x + viii

f'(ten) = 8x + 12

Now we take to find the instantaneous charge per unit of modify at 10 = 4

f(four) = 8x + 12

f(four) = viii(4) + 12

f(4) = 44