How To Find The Maximum Height Of A Function

I studied applied mathematics, in which I did both a available'south and a master's degree.

Finding the minimum or maximum of a function can be very useful. Information technology oft comes upwards in optimization bug that do not have constraints, or in which the constraints do non forestall the function from reaching its minimum or maximum.

These types of issues occur a lot in practice. An example would be determining the cost of a certain commodity. If you lot know the demand for a given price (or a good estimation of the demand), you can summate the price for which you volition make the well-nigh profit. This can be formulated as finding the maximum of the profit function.

The minimum and maximum of a office are too chosen farthermost points or extreme values of the function. They can exist local or global .

Local and Global Extrema

A local minimum/maximum is a point in which the part reaches its lowest/highest value in a certain region of the function. In formal words, this ways that for every local minimum/maximum x, there is an epsilon such that f(x) is smaller/greater than all values f(y) for all y that have altitude at most epsilon to x. That looks very complicated but information technology does hateful as much as f(x) is the smallest/largest value for all points close to x. At that place might be values, nonetheless, that are smaller/larger than the local minimum/maximum, but they are further away.

The global minimum is the smallest value the function takes on in its entire domain. Equivalently, the local maximum is the largest value of the function. Therefore, every global extreme point is also a local extreme betoken, just the opposite is not true.

Do All Functions Have a Minimum and a Maximum?

A function does not necessarily have a minimum or maximum. For example, the office f(ten) = x does not have a minimum, nor does information technology have a maximum. This tin can be seen easily equally follows. Suppose the role has a minimum at x = y. Then fill in y-1 and the function has a smaller value. Therefore we have a contradiction and y was not the minimum, and hence the minimum does not exist. An equivalent proof can exist given for the maximum.

The function f(ten) = 10² does have a minimum, namely at x = 0. This is easily verified since f(x) tin can never become negative, since it is a square. At x = 0, the role has value 0, so this must be the minimum. It does not have a maximum, which tin be proven using the exact same argument equally nosotros used before.

How to Discover the Farthermost Points of a Function

At a local minimum, the role changes direction. This is because it is the everyman point in its neighborhood. Therefore the slope of the part goes from negative to positive, since the part was decreasing until it reached the minimum and then it started increasing again. This means that in the local minimum, the gradient is equal to zero, and hence the derivative of the function must exist equal to zero in the point that is the minimum. The same holds for the local maximum of a role, since there the function goes from increasing to decreasing.

Therefore, to find the location of the local maxima and local minima you have to solve the equation f'(x) = 0. Therefore y'all have to offset find the derivative of the function. If you are non familiar with the derivative, or if you would similar to know more nigh it I recommend reading my article about finding the derivative of a function. For this article I assume the derivative is known.

Math: What Is the Derivative of a Function and How to Summate It?

Afterwards you have solved the equation f(x)= 0, you take found the locations at which the extrema are located. To observe the value of the extrema you demand to fill in the location in the office. From the solutions you can not straight encounter whether it is a local minimum or a local maximum, since both are solutions to the same equation. Therefore, you have to plot the function to determine this.

Besides, yous cannot say directly if you have constitute a global minimum or maximum, or if it is only local. Also, yous can decide this with the aid of the plot of the function.

An Example

Equally an example, nosotros will utilise the role f(x) = 1/three xⁱⁱⁱ- 4x. Outset nosotros calculate the derivative of the function, which is:

f'(x) = xⁱⁱ - 4

Scroll to Proceed

Read More than From Owlcation

Then nosotros solve f'(ten) = 0:

10^two+ 4 = 0

This gives ten = 2 or x = -2. Therefore nosotros know that the local extrema are located at ii and -2. We fill both in to determine the value of the extrema:

ane/3 two³- 4*2 = 8/iii - 8 = -16/3

1/3 (-two)³- 4*-2 = -8/three + 8 = 16/3

And then we plot the office.

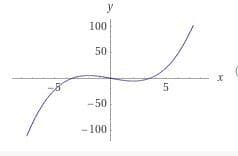
Plot of 1/3*x^3 -4x — Plot of one/iii*x^3 -4x

Every bit you can see in the plot, at x=-2 we accept a local maximum with value 16/3. At x=2 we take a local minimum with value -16/iii. We can too meet however, that both local extrema are not global, since conspicuously there are points at which the function value is smaller than -16/3 and also there are points at which the function value is larger than 16/three. This means that the global minimum and global maximum exercise not be, even though there do exist local extrema, which can happen.

Solving f'(x) = 0

Here, f'(x) was a quadratic function, which means nosotros had to find the roots of a quadratic part to find the local extrema. Hither I did not go deep into how I did solve this, but I did write an commodity near how to solve these kind of equations.

Math: How to Detect the Roots of a Quadratic Function

Another example is f(x) = sin(ten). Then f'(x) = cos(10), which is zero at ±pi/ii, ±2pi/ii, ±3pi/2, ....

At these points, the function values are -ane and one alternating. This means that there are infinitely local minima with value -1 and infinitely many local maxima with value 1. Since the function is nowhere smaller than -1 and nowhere larger than 1 all these local extrema are global. Then this is an case of a role where the global minimum and global maximum do exists and are not unique.

Summary

A minimum or a maximum is chosen an farthermost point. A local farthermost point is the smallest or largest value in its neighborhood. If information technology is also the smallest or largest at the unabridged domain of the function, it is called a global extreme point.

The local minima and maxima can be found by solving f'(x) = 0. Then using the plot of the function, you can determine whether the points you find were a local minimum or a local maximum. Also, you lot can make up one's mind which points are the global extrema.

Not all functions have a (local) minimum/maximum. And even if a role has a local minimum, it tin happen that a global minimum does not be. The same holds for the maximum. Also, the global minimum and maximum do not take to be unique. It might happen that at multiple points the part reaches its smallest or largest value.

This content is accurate and true to the best of the author's noesis and is non meant to substitute for formal and individualized advice from a qualified professional person.

Umesh Chandra Bhatt from Kharghar, Navi Mumbai, Bharat on December 06, 2020:

Well explained.

Source: https://owlcation.com/stem/Math-How-to-Find-the-Minimum-and-Maximum-of-a-Function

Posted by: fullercultin.blogspot.com